Big O Asymptotic Analysis
2020-08-03
If you have ever applied for a job at a Tech company or if you offered Computer Science in the university, there is a probability you have come across the term Big O. The term is Big O Asymptotic Analysis but is more popularly known as the Big O Notation (You can definitely use the term Big O Asymptotic Analysis just to show off when talking to friends 😉)
Qualities of Good Code
Before defining what Big O is, I would like to talk about two very important qualities of good code. They are readability and scalability.
Readability
This simply refers to how easy it is for your code to be read and understood by others.
Scalability
I like to think of scalability like this. Given n inputs or elements, by how much will your code slow down or perform as n increases. The slower the code slows down, the better it is. If its not completely clear right now, don't worry. You'll get it as we move along.
When we talk about scalability of code, two main properties come to mind:
- Speed
- Memory
The main idea is to write code that's fast and consumes little memory. Unfortunately, its not that simple. Code that is extremely fast can end up consuming more memory. On the other hand, you can have a code that consumes less memory which is very slow. The key is to find the right balance in order to obtain optimum efficiency.
Why The Need For Big O
You may be thinking, "So how do I know how well my code performs given as the inputs vary ?" Enter Big O Notation. The Big O notation is used to describe the performance and complexity of an algorithm. It basically defines the time required or space needed to successfully execute an algorithm. Being able to determine this enables one to know the usefulness of a particular algorithm or code.
The amount of time required to run an algorithm is called its time complexity. The amount of space needed by that algorithm to run is called its space complexity.
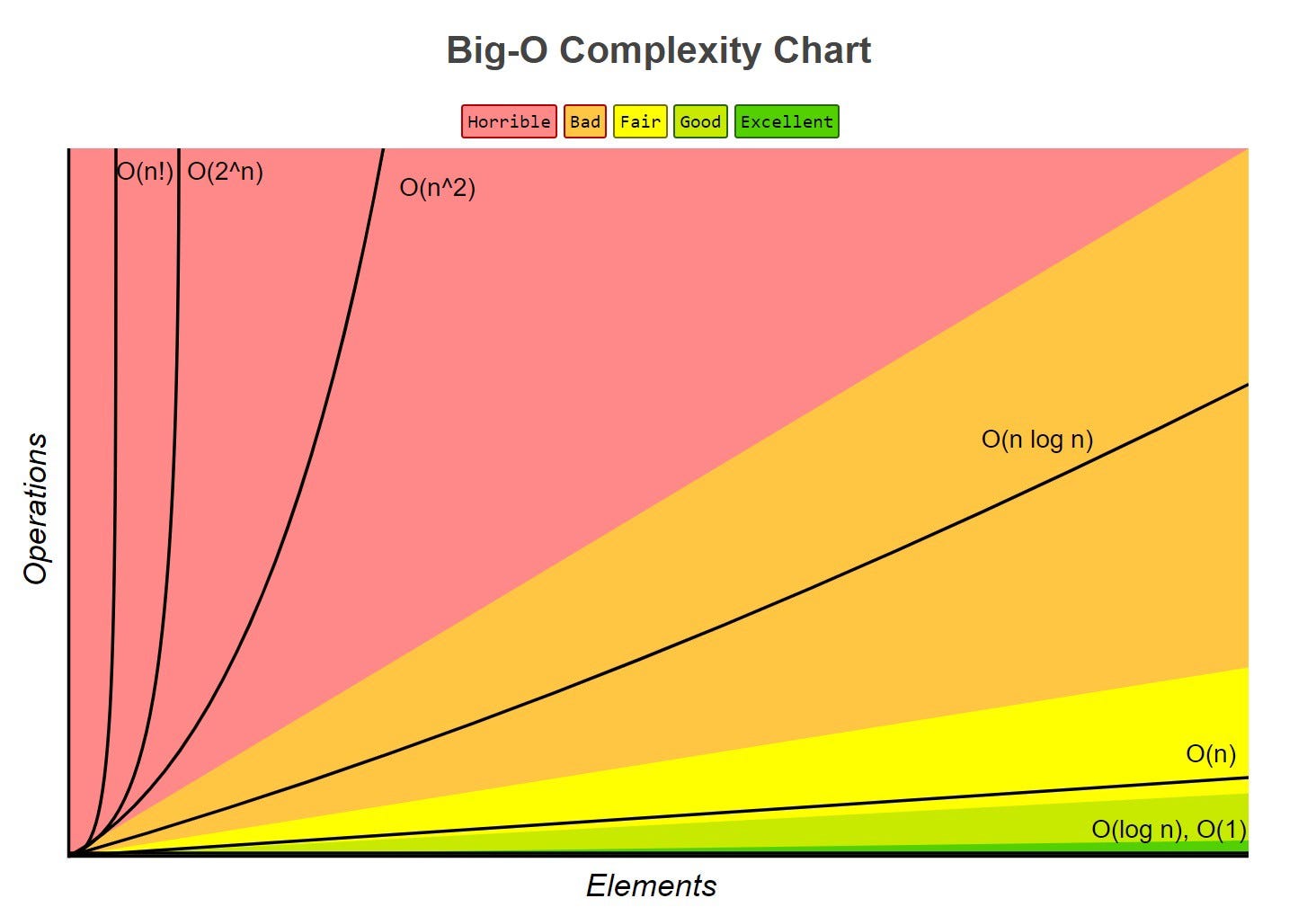
Below are some of the most common time and space complexities:
- Constant Runtime (O(1))
- Linear Runtime (O(n))
- Logarithmic Runtime (O(logn))
- Linear Runtime (O(n))
- Quadratic Runtime (O(n2))
- Exponential Runtime (O(2n))
- Factorial Runtime (O(n!))
- Super-linear Runtime- (O(nlogn))
The following chart shows how each runtime varies as the number of elements increase
We will discuss the most common runtimes one after another as time goes by so that you at least get a fair idea of each of them. I will also try to keep each post as short as possible.Till then, Happy coding! 👊